Question

The car contains 50,000 rods. Claude Ong, manager of Quality Assurance, directs his crew measure the lengths of 100 randomly selected rods. If the population of rods have a mean length of 120 inches and a standard deviation of 0.05 inch, the probability that Claude's sample has a mean less than 119.985 inches is

A) 0.9974
B) 0.0026
C) 0.4987
D) 0.0013
E) 0.0030

Answer 1

Answer: D) 0.0013

Explanation:

Let x be the random variable that represents the lengths of rods.

As pr given , we have

n=100 ,
`\mu=120\ inches`
`\sigma=0.05\ inch`

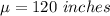
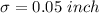
z-score :
`z=(x-\mu)/((\sigma)/(√(n)))`

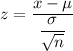
For x= 119.985 inches , we have

`z=(119.985 -120)/((0.05)/(√(100)))=-3`

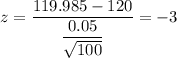
Using the standard z-table , we have

The probability that Claude's sample has a mean less than 119.985 inches is

`P(z<-3)=1-P(z<3)\\\\=1-0.9986501\\\\=0.0013499\approx0.0013`

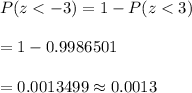
Hence, the probability that Claude's sample has a mean less than 119.985 inches is 0.0013.