Answer: D) 0.0013
Explanation:
Let x be the random variable that represents the lengths of rods.
As pr given , we have
n=100 ,
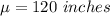
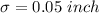
z-score :
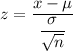
For x= 119.985 inches , we have
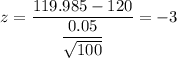
Using the standard z-table , we have
The probability that Claude's sample has a mean less than 119.985 inches is
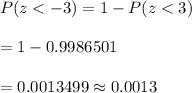
Hence, the probability that Claude's sample has a mean less than 119.985 inches is 0.0013.