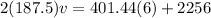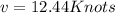Question

A ship leaves a port at noon and travels due west at 20 knots. At 6 PM, a second ship leaves the same port and travels northwest at 15 knots. How fast are the two ships moving apart when the second ship has traveled 90 nautical miles?

Answer 1

`v = 12.44 Knots`

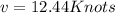
Step-by-step explanation:

First ship starts at Noon with speed 20 Knots towards West

now we know that 2nd ship starts at 6 PM with speed 15 Knots towards North West

so after time "t" of 2nd ship motion the two ships positions are given as

`r_1 = 20(t + 6)\hat i`

`r_2 = 15(t)(cos45\hat i + sin45\hat j)`

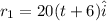
now we can find the distance between two ships as

`x = √((20(t + 6) - 10.6 t)^2 + (10.6t)^2)`

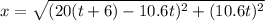
now we have

`x^2 = (120 + 9.4 t)^2 + (10.6 t)^2`

`x^2 = 200.72 t^2 + 14400 + 2256 t`

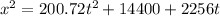
now we will differentiate it with respect to time

`2x(dx)/(dt) = 401.44 t + 2256`

here we know that

`t = (90)/(15) = 6 hours`

so we have

`x = 187.5`

now we have

`2(187.5) v = 401.44(6) + 2256`

`v = 12.44 Knots`