Question

The "cold start ignition time" of an automobile engine is being investigated by a gasoline manufacturer. The following times (in seconds) were obtained for a test vehicle: 1.75, 1.92, 2.62, 2.35, 3.09, 3.15, 2.53, 1.91. (a) Calculate the sample mean, sample variance, and sample standard deviation. (b) Construct a box plot of the data.

Answer 1

(a) Sample mean = 2.42

Sample variance = 0.29

Sample standard deviation = 0.53

(b) Please see the picture below

Explanation:

(a) 1. Calculate the sample mean:

To calculate the sample mean take all the times and divide them between the number of items of the sample:

`x=(1.75+1.91+1.92+2.35+2.53+2.62+3.09+3.15)/(8)`

`x=2.42`

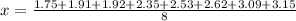
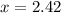
2. Calculate the sample variance:

To calculate the sample variance lets to name the items as the following:

`x_(1)=1.75`

`x_(2)=1.91`

`x_(3)=1.92`

`x_(4)=2.35`

`x_(5)=2.53`

`x_(6)=2.62`

`x_(7)=3.09`

`x_(8)=3.15`

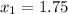
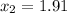
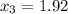
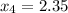
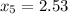
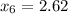
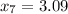
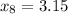
So, the formula to calculate the sample varianza is:

`s^(2)=((x_(1)-x)^(2)+(x_(2)-x)^(2)+(x_(3)-x)^(2)+(x_(4)-x)^(2)+(x_(5)-x)^(2)+(x_(6)-x)^(2)+(x_(7)-x)^(2)+(x_(8)-x)^(2))/(n-1)`

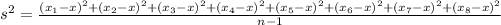
where n is the number of items of the sample and x is the sample mean.

Replacing values:

`s^(2)=((-0.67)^(2)+(-0.51)^(2)+(-0.5)^(2)+(-0.07)^(2)+(0.11)^(2)+(0.2)^(2)+(0.67)^(2)+(0.73)^(2))/(7)`

`s^(2)=((0.4489+0.2601+0.25+0.0049+0.0121+0.04+0.4489+0.5329)/(7)`

`s^(2)=((0.4489+0.2601+0.25+0.0049+0.0121+0.04+0.4489+0.5329)/(7)`

`s^(2)=0.29`

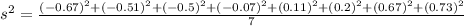
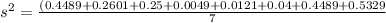
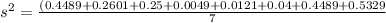
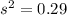
3. Calculate the sample standard deviation:

The standard deviation is the square root of the variance, so:

`d=√(0.29)`

`d=0.53`

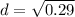
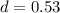
(b) (1) To construct a box plot of the data, first sort the data from the smallest to the largest:

1.75 1.91 1.92 2.35 2.53 2.62 3.09 3.15

(2) Find the median of the data.

As n is an odd numer the median will be the mean of the two data of the center:

`median=(2.35+2.53)/(2)`

`median=2.44`

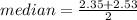
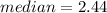
(3) Find the first quartile:

`firstquartile=(1.91+1.92)/(2)`

`firstquartile=1.915`

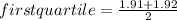
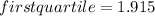
(4) Find the third quartile:

`thirdquartile=(2.62+3.09)/(2)`

`thirdquartile=2.855`

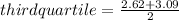
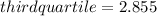
(5) Draw the median, first and third quartile and make a box. Then draw the smallest and largest values of the data and draw a line to conect the box. (Please see the picture below)