Question

Solve this linear system using determinants

2x + 3y = 6
- 8x - 3y = 12
A1 =
4=
4yl=
DONE

Answer 1

The value of X = 3 And Y = 4

Explanation:

Given the linear system as :

2x + 3y = 6

-8x - 3y = 12

Apply Determinant method :

Dx =
`\begin{bmatrix}3 &6 \\ -3 & 12\end{bmatrix}`

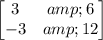
Dy =
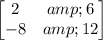
`\begin{bmatrix}2 &6 \\ -8 & 12\end{bmatrix}`

D =
`\begin{bmatrix}2 &3 \\ -8 & -3\end{bmatrix}`

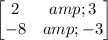
Or Dx = ( 36 + 18) = 54 Dy = (24 + 48) = 72 D = ( -6 +24) = 18

So, X =
`(Dx)/(D)` =
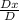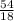`(54)/(18)` = 3

And Y =
`(Dy)/(D)` =
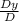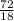`(72)/(18)` = 4

Hence the value of X = 3 And Y = 4 Answer