Answer:
The value of X = 3 And Y = 4
Explanation:
Given the linear system as :
2x + 3y = 6
-8x - 3y = 12
Apply Determinant method :
Dx =
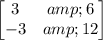
Dy =

D =
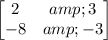
Or Dx = ( 36 + 18) = 54 Dy = (24 + 48) = 72 D = ( -6 +24) = 18
So, X =
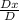 =
=
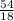 = 3
= 3
And Y =
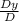 =
=
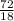 = 4
= 4
Hence the value of X = 3 And Y = 4 Answer