Answer:
in both the cases the time will be same
Step-by-step explanation:
As we know that the chunk is projected horizontally
so here the initial speed of the chunk is given as

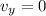
now in order to reach the ball to the ground we can say
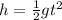
so we will have

now if another ball is just dropped from the same height then its initial speed is also zero in both direction
so again we have
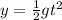

so we can say that in both the cases the time will be same