Question

The equation of a circle in general form is

x2 + y2 + 20x + 12y + 15 = 0.
What is the equation of the circle in standard form?
• (x + 10)² + (y+6)2 = 121
• (x + 20)² + (y + 12)2 = 225
• (x + 10)² + (y+6)2 = 225
(x+ 20)² + (y + 12) = 121
inicl

Answer 1

The answer to this would be your first option!!

• (x + 10)² + (y+6)2 = 121

Hope this helped, have a blessed day!!

Answer 2

• (x + 10)² + (y+6)² = 121

Explanation:

For this case we have the following expression:

`x^2 + y^2 +20 x + 12y +15=0`

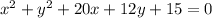
And we want to write this on this general way:

`(x-h)^2 +(y-k)^2 = r^2`

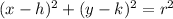
So on this case we need to complete the squares like this:

`x^2 + 20 x + ((20)/(2))^2 + y^2 + 12y + ((12)/(2))^2 +15 =((20)/(2))^2+((12)/(2))^2`

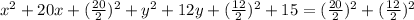
Now we can subtract from both sides 15 and we got:

`(x^2 + 20 x +100) + (y^2 + 12y +36) = 100+36 - 15`

`(x+10)^2 +(y+6)^2 = 121`

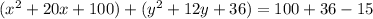
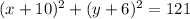
And we can write the last expression like this:

`(x-(-10))^2 +(y-(-6))^2 = 121`

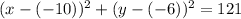
And if we compare to the general expression we see that:

`h = -10 , k = -6, r=√(121)=11`

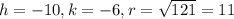
So the correct option for this case would be:

• (x + 10)² + (y+6)² = 121