Answer:
• (x + 10)² + (y+6)² = 121
Explanation:
For this case we have the following expression:
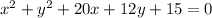
And we want to write this on this general way:
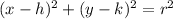
So on this case we need to complete the squares like this:
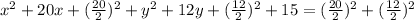
Now we can subtract from both sides 15 and we got:
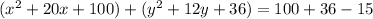
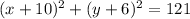
And we can write the last expression like this:
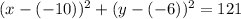
And if we compare to the general expression we see that:
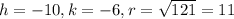
So the correct option for this case would be:
• (x + 10)² + (y+6)² = 121