Answer:
a) 0.222
b)0.037
c)0.549
Explanation:
Let's start defining the random variable ⇒
X : ''The number of missing pulses''
X can be modeled as a Poisson random variable.
X ~ Po(λ)
In a Poisson distribution : μ = λ
Where μ is the mean of the variable.
X ~ Po(0.3)
The probability function for a Poisson random variable is :
In the equation I replace λ = m
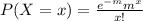
Where P(X=x) is the probability of the random variable X to assume the value x
e is the euler number
m = λ is the mean of the variable
In this exercise :
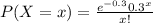
is the probability function.
For a)

For b)
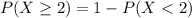
![P(X\geq 2)=1-[P(X=0)+P(X=1)]](https://img.qammunity.org/2020/formulas/mathematics/college/b8pdf3kh89l9dxtmt5csgv22891gwal24q.png)
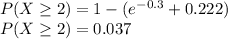
c)
Let's define A :''a disk doesn't contain a missing pulse''
We are looking for P(A1∩A2) of two different disk don't have a missing pulse.
Because of the independence we can write this probability as
P(A1∩A2)= P(A1).P(A2)
The probability of a random disk to don't have a missing pulse is P(X=0)
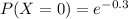 ⇒
⇒
![P(A1).P(A2)=[P(X=0)].[P(X=0)]](https://img.qammunity.org/2020/formulas/mathematics/college/hfh355nev0p4hznugq7pzrgjg36lw80u0g.png)
![[P(X=0)].[P(X=0)]=(e^(-0.3))(e^(-0.3))=0.549](https://img.qammunity.org/2020/formulas/mathematics/college/hm3fjabedciaf95u78trina79tvz9no4xp.png)