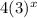Find the exponential function passing through points (-1,4/3) and (3,108)

Question

asked Feb 7, 2020 88.6k views

2 Answers

Karthik Manchala · Answer 1 · 2020-02-13T06:41:18+0000

Answer:

An exponential function is in the general form
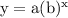
$\mathrm{y}=\mathrm{a}(\mathrm{b})^{\mathrm{x}}$

Step-by-step explanation:

(x,y) = (-1,4/3) and (x,y)= (3,108) are the given functions

Therefore,

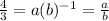
(4)/(3)=a(b)^(-1)=(a)/(b)

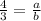(4)/(3)=(a)/(b) - eq(1)

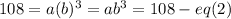
108=a(b)^(3)=a b^(3)=108-e q(2)

Multiply both sides of the first equation by b to find that

(4)/(3) b=a

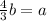
Substituting in eq-2 we get

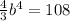
(4)/(3) b^(4)=108

b^(4)=81

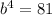
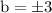
$\mathrm{b}=\pm 3$

$\mathrm{b}=+3, \text { then } 108=\mathrm{a}(3)^(3)$

which gives a = 4,

henceforth the equation becomes as
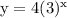
$\mathrm{y}=4(3)^{\mathrm{x}}$

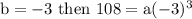
$\mathrm{b}=-3 \text { then } 108=\mathrm{a}(-3)^(3)$

which gives a = -4,

henceforth the equation becomes as y =
-4(-3)^(x)

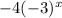
However! In an exponential function, b>0, otherwise many issues arise when trying to graph the function.

The only valid function is