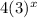Answer:
An exponential function is in the general form
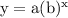
Step-by-step explanation:
(x,y) = (-1,4/3) and (x,y)= (3,108) are the given functions
Therefore,
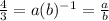
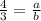 - eq(1)
- eq(1)
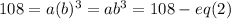
Multiply both sides of the first equation by b to find that
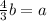
Substituting in eq-2 we get
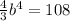
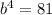
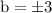
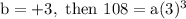
which gives a = 4,
henceforth the equation becomes as
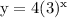
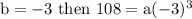
which gives a = -4,
henceforth the equation becomes as y =
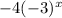
However! In an exponential function, b>0, otherwise many issues arise when trying to graph the function.
The only valid function is