The equation of the line that is perpendicular to 4x - 3y = 10 through the point (-2,4) is
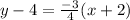
Solution:
Given, line equation is 4x – 3y = 10
We have to find a line that is perpendicular to 4x – 3y = 10 and passing through (-2, 4)
Now, let us find the slope of the given line,
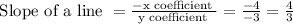
We know that, slope of a line
 slope of perpendicular line = -1
slope of perpendicular line = -1

Now, slope of our required line =
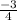 and it passes through (-2, 4)
and it passes through (-2, 4)
The point slope form is given as:
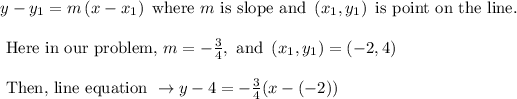
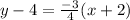
Hence the equation of line is found out