Question

State the equation of the line

that is perpendicular to 4x-3y=10
through the point (-2,4)

Answer 1

The equation of the line that is perpendicular to 4x - 3y = 10 through the point (-2,4) is
`y-4=(-3)/(4)(x+2)`

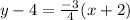
Solution:

Given, line equation is 4x – 3y = 10

We have to find a line that is perpendicular to 4x – 3y = 10 and passing through (-2, 4)

Now, let us find the slope of the given line,

`\text { Slope of a line }=\frac{-\mathrm{x} \text { coefficient }}{\mathrm{y} \text { coefficient }}=(-4)/(-3)=(4)/(3)`

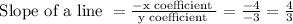
We know that, slope of a line
`*` slope of perpendicular line = -1

`\begin{array}{l}{\text { Then, } (4)/(3) * \text { slope of perpendicular line }=-1} \\\\ {\rightarrow \text { slope of perpendicular line }=-1 * (3)/(4)=-(3)/(4)}\end{array}`

Now, slope of our required line =
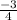`(-3)/(4)` and it passes through (-2, 4)

The point slope form is given as:

`\begin{array}{l}{y-y_(1)=m\left(x-x_(1)\right) \text { where } m \text { is slope and }\left(x_(1), y_(1)\right) \text { is point on the line. }} \\\\ {\text { Here in our problem, } m=-(3)/(4), \text { and }\left(x_(1), y_(1)\right)=(-2,4)} \\\\ {\text { Then, line equation } \rightarrow y-4=-(3)/(4)(x-(-2))}\end{array}`

`y-4=(-3)/(4)(x+2)`

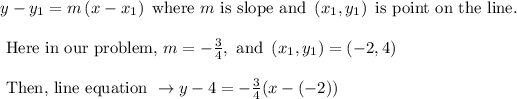
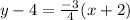
Hence the equation of line is found out