Answer:
a) The discriminant of the equation = - 44
b)The nature of the roots will be imaginary.
c)

Explanation:
Here, the given expression is
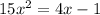
or,
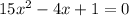
Now the discriminant (D) of a quadratic equation

D =
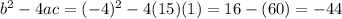
Hence, the discriminant of the equation = - 44
As D< 0, so the roots will be imaginary.
Now,by quadratic formula :
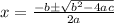
So, here
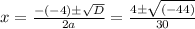
So, either
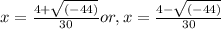
or,
