Question

to masses 7 kg and 12 KG are connected at the two ends of a light inextensible string that passes over a fictional Pulley using free body diagram method find acceleration of masses and the tension in the string when the masses are released ​

Answer 1

Tension in the string when the masses are released ​is 88.42 N

Acceleration of masses is
`\bold{a=2.578 m/sec^2}`

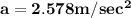
Explanation:

Given:

Mass ,m1 = 12

Mass , m2 = 7

g =
`9.8m/s^2`

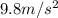
To Find :

Tension in the string=?

Acceleration of masses=?

Solution:

For mass M_1

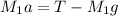`M_1 a=T-M_1 g`--------------------(1)

For mass M2

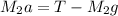`M_2 a=T-M_2 g`---------------------(2)

Adding equation (1) and (2)

`(M_1+M_2)a=(M_2-M_1)g`

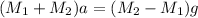
Finding Acceleration:

Acceleration is given by

`a=(M_2-M_1 )/(M_1+M_2) g`

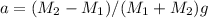
Substituting the values,

`a=((12-7)(9.8))/((7+12))`

`a=((5)(9.8))/(19)`

`a=\frac {49}{19}`

`a=2.578 m/sec^2`

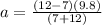
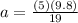
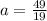
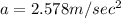
Finding Tension:

From Equation 1

`M_1 a=T-M_1 g`

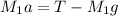
Tension can be

`T=M_1 a+M_1 g`

T=(7)(2.578) + 7(9.8)

T=(17.99)+(68.6)

T=86.59 N