Tension in the string when the masses are released is 88.42 N
Acceleration of masses is
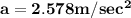
Explanation:
Given:
Mass ,m1 = 12
Mass , m2 = 7
g =
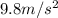
To Find :
Tension in the string=?
Acceleration of masses=?
Solution:
For mass M_1
 --------------------(1)
--------------------(1)
For mass M2
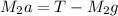 ---------------------(2)
---------------------(2)
Adding equation (1) and (2)
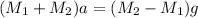
Finding Acceleration:
Acceleration is given by
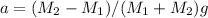
Substituting the values,
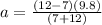

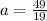

Finding Tension:
From Equation 1

Tension can be
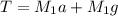
T=(7)(2.578) + 7(9.8)
T=(17.99)+(68.6)
T=86.59 N