Question

Starting from Newton's second law, explain how a collision that is free from external forces conserves momentum. In other words, explain how the momentum of the system remains constant with time. Newton's second law states that the acceleration of each object, which is proportional to each object's change in momentum, is proportional to the sum of the forces on the object. In the absence of external forces,

Answer 1

From Second law of Newtons:

It states that rate of change of linear momentum is equal to the total external force.

We can say that

`F_(ext)=(dP)/(dt)`

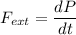
Linear momentum P

P = m v

m=Mass ,v =velocity

`F_(ext)=(dP)/(dt)`

`F_(ext)=(d(mv))/(dt)`

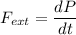
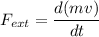
If mass is not varying with time

`F_(ext)=m(dv)/(dt)`

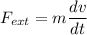
We know that acceleration a

`a=(dv)/(dt)`

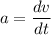
So

`F_(ext)=ma`

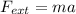
Again

`F_(ext)=(dP)/(dt)`

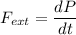
If External force is zero then

`0=(dP)/(dt)`

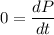
It means that P is not varying with time and it is constant.

So

Pi = Pf ( Initial linear momentum = Final linear momentum)

Linear momentum is conserve.

Answer 2

In the absence of external forces, the momentum remains conserved.

Step-by-step explanation:

Newton's second law of motion explains how the momentum of the system remains constant with time. It explains that the acceleration of each object, is directly proportional to object's change in momentum.

While in the absence of external forces such that,

`F_(ext)=0`

`F_1+F_2=0`

So, the initial momentum is equal to the final momentum of two objects. It shows the law of conservation of momentum.