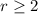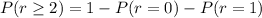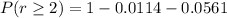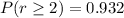Question

Police records in the town of Saratoga show that 17 percent of the drivers stopped for speeding have invalid licenses. If 24 drivers are stopped for speeding. (a) Find the probability that none will have an invalid license. (Round your answer to 4 decimal places.) Probability (b) Find the probability that exactly one will have an invalid license. (Round your answer to 4 decimal places.) Probability (c) Find the probability that at least 2 will have invalid licenses. (Round your answer to 4 decimal places.) Probability

Answer 1

Explanation:

Given

17 % of the drivers stopped have invalid licenses

n=24 drivers are stopped

using Binomial distribution

`^nC_r(p)^r(q)^(n-r)`

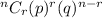
here p=0.17

q=1-0.17=0.83

(a)none will have valid license i.e. r=0

`P(r=0)^(24)C_0(0.17)^0(0.83)^(24)=(0.83)^(24)=0.0114`

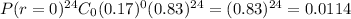
(b)Exactly one have invalid license i.e. r=1

`P(r=1)=^(24)C_1(0.17)^1(0.83)^(23)=24* 0.17* (0.83)^(23)`

`=0.0561`

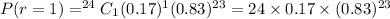
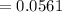
(c)At least 2 will have invalid license i.e.
`r\geq 2`

`P(r\geq 2)=1-P(r=0)-P(r=1)`

`P(r\geq 2)=1-0.0114-0.0561`

`P(r\geq 2)=0.932`