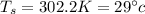Question

he Weather Channel reports that it is a hot, muggy day with an air temperature of 90????F, a 10 mph breeze out of the southwest, and bright sunshine with a solar insolation of 400 W/m2. Consider the wall of a metal building over which the prevailing wind blows. The length of the wall in the wind direction is 10 m, and the emissivity is 0.93. Assume that all the solar irradiation is absorbed, that irradiation from the sky is negligible, and that flow is fully turbulent over the wall. Estimate the average wall temperature.

Answer 1

29\°c

Step-by-step explanation:

We need to define a couple of properties

`T_f = 305KP= 1atm\\v=16.27*10^(-6)m^2/s\\k=0.02658W/mK\\Pr=0.707`

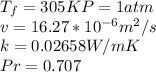
For this problem I took Steady-state conditions with isothermal temperature in
`T_s`

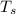
As well as a flow turbulent over the wall and negligible heat transfer into the building.

We start making a energy balance on the wall,

`E'_(in)-E'_(out)=0`

`-q'_(cv)+(\alpha_S G_S-E_S)L=0`

`-\bar{h}_L L(T_s-T_(\infty))+(\alpha_S G_S - \epsilon \sigma T_s^4)L = 0`

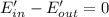
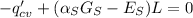
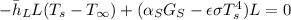
Again, assuming fully turbulent flow over the leng of the wall,

`\bar{Nu}_L = \frac{\bar{h}_L}{k} = 0.037 Re_L^(4/4) Pr^(1/3)`

`Re_L = u_(\infty)(L)/(v) = 4.47*(10)/(16.27*10^(-6))= 2.748*10^6`

`\bar{h}_L = (0.02658/10)0.037(2.748*10^6)^(4/5)(0.707)^(1/3)=12-4W/m^K`

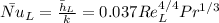
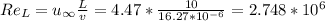
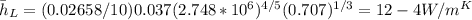
Substituting to fin
`T_s,`

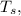
`-12.4W/m^2*10m[T_s-(32.2+273)]K+[1*400W/m^2-0.93*5.67*10^(-8)W/m^2.K^4T_s^4]*10m=0`

`T_s=302.2K=29\°c`