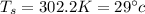Answer:
29\°c
Step-by-step explanation:
We need to define a couple of properties
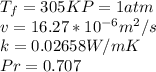
For this problem I took Steady-state conditions with isothermal temperature in
As well as a flow turbulent over the wall and negligible heat transfer into the building.
We start making a energy balance on the wall,
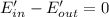
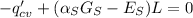
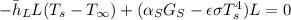
Again, assuming fully turbulent flow over the leng of the wall,
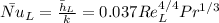
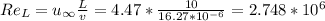
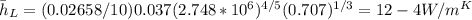
Substituting to fin
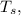
![-12.4W/m^2*10m[T_s-(32.2+273)]K+[1*400W/m^2-0.93*5.67*10^(-8)W/m^2.K^4T_s^4]*10m=0](https://img.qammunity.org/2020/formulas/engineering/college/oc0thyjbtlkq536pkmx5cerdpgan9p3izw.png)