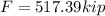Question

Water at 60˚F flows through a nozzle that contracts from a diameter of 3 in. to 0.5 in. The pressure at section 1 is 2500 psfg, and atmospheric pressure prevails at the exit of the jet. Calculate (a) the speed of the flow at the nozzle exit and (b) the force required to hold the nozzle stationary. Neglect weight.

Answer 1

Let's start by getting the expressions for the speed that allow us to get the equations correctly,

`A_1V_1 = A_2V_2`

`((\pi)/(4)*d^2_1)(V1) = ((\pi)/(4)*d^2_2)(V_2)`

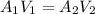
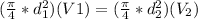
Then,

`(V_1)/(V_2)= (d^2_2)/(d^2_1)`

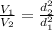
Replacing then

`(V_1)/(V_2) = ((0.5^2)/(3.0^2))`

`(V_1)/(1/36) = V_2`

`V_2 = 36.0V_1`

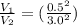
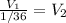
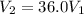
We then proceed to obtain the speed, from the previously given relationship,

So,

`p_1+(\rho V^2_1)/(2) = p_2 + (\rho V^2_2)/(2)`

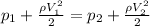
Where
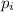`p_i` is the pressure in each section,

As section 2 is open, then
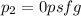`p_2=0psfg` and
`\rho = 1.94slugs/ft^3`

`2,500+(1.94(V_1)^2)/(2) = 0 + (1.94(36V_1)^2)/(2)`

`2,500+1.94*0.5V^2_1 = 1.94*(648)V^2_1`

`2,500 = 1.94*(647.5)V^2_1`

`V_1 = \sqrt{(2,500)/(1.94*647.5)}`

`V_1 = 1.4101ft/s`

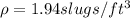
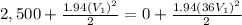
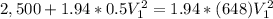
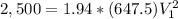
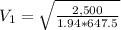
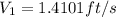
a) The velocity at section 2 would be,

`V_2 = 36V_1`

`V_2 = 36*(1.4101)`

`V_2 = 50.78ft/s`

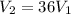
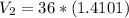
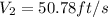
b) The discharge Q would be,

`Q= 1.4101*((\pi)/(4)*(0.5)^2)`

`Q= 0.2768 ft^3/s`

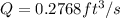
The force then is,

`F+P_1A_1-P_2A_2 = \rho Q (V_2-V_1)`

`F - 2,500*((\pi)/(4)(0.5)^2)= 1.94*0.2768*(50.78-1.4101)`

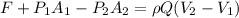
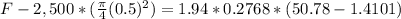
Solving,

`F= 517.39kip`