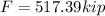Let's start by getting the expressions for the speed that allow us to get the equations correctly,
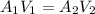
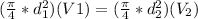
Then,
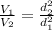
Replacing then
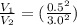
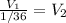
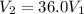
We then proceed to obtain the speed, from the previously given relationship,
So,
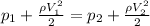
Where
 is the pressure in each section,
is the pressure in each section,
As section 2 is open, then
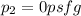 and
and
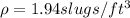
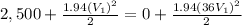
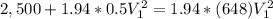
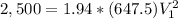

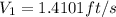
a) The velocity at section 2 would be,

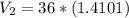
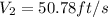
b) The discharge Q would be,

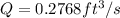
The force then is,
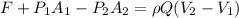
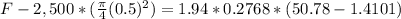
Solving,