Answer:
1. 758 newborn babies
2. 918 newborn babies
3. 756 newborn babies
4. 587 newborn babies
Explanation:
Let's start by defining the following event :
W : ''The weight of a newborn baby''
W ~ N(μ,σ) Where N is the normal distribution, μ is the mean and σ is the standard deviation
W ~ N(6.2,2)
To calculate probability, we need to turn this variable into a N(0,1) by doing the following :
First we subtract the mean to W and then we divide by the standard deviation
[(W-μ) / σ] ~ N(0,1)
1.
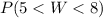
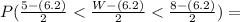

Where Z ~ N(0,1)
 is the area below the normal curve N(0,1) between the values -0.6 and 0.9
is the area below the normal curve N(0,1) between the values -0.6 and 0.9
P(-0.6<Z<0.9) = Φ(0.9) - Φ(-0.6)
Where Φ is the cumulative distribution for N(0,1)
P(-0.6<Z<0.9) = Φ(0.9) - Φ(-0.6) = 0.8159 - 0.2743 = 0.5416
Then the probability of the variable W to be between 5 and 8 pounds is 0.5416
To find the number of newborn babies expected to weigh between 5 and 8 pounds we multiply the group of 1400 and the probability
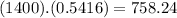
758.24 ≅ 758
Then 758 newborn babies are expected to weigh between 5 and 8 pounds
2.
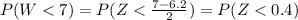
P(Z<0.4) = Φ(0.4) = 0.6554
The expected number of newborn babies is

917.56 ≅ 918
918 newborn babies are expected to weigh less than 7 pounds
3.
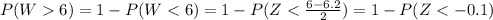
1-P(Z<-0.1) = 1 - Φ(-0.1) = 1 - 0.4602 = 0.5398
The expected number of babies is
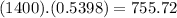
755.72 ≅ 756
The expected number of babies to weigh more than 6 pounds is 756
4.
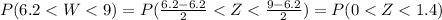
P(0<Z<1.4) = Φ(1.4) - Φ(0) = 0.9192 - 0.500 = 0.4192
The expected number of babies is
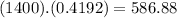
586.88 ≅ 587
587 newborn babies are expected to weigh between 6.2 and 9 pounds