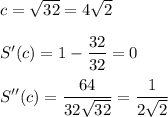Question

The product of two numbers is 32. Find the sum of the two numbers S(x) as a function of one of the numbers, x. S(x) = Find the positive numbers that minimize the sum and list them in increasing order: (smaller number) = ?(larger number) = ?Let c be the smaller of the two numbers that minimize the sum. Then c = ?S'(c) = ? and S"(c) = ?

Answer 1

`c = 4\sqrt2\\\\S'(4\sqrt2) = 0\\\\S''(4\sqrt2)=(1)/(2\sqrt2)`

Explanation:

We are given the following information in the question:

The product of two numbers is 32.

Let the two numbers be x and y, then,

`x* y = 32\\\\y = \displaystyle(32)/(x)`

The sum of the two numbers = S(x)

`S(x) = x + \displaystyle(32)/(x)`

First, we differentiate S(x) with respect to x, to get,

`\displaystyle(d(S(x)))/(dx) = (d( x +(32)/(x)))/(dx) = 1 - (32)/(x^2)`

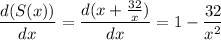
Equating the first derivative to zero, we get,

`(d(S(x)))/(dx) = 0\\\\1 - (32)/(x^2)= 0`

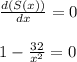
Solving, we get,

`x =\pm √(32)`

Again differentiation S(x), with respect to x, we get,

`\displaystyle(d^2(S(x)))/(dx^2) =(64)/(x^3)`

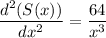
At
`x =√(32)`,

`(d^2(S(x)))/(dx^2) > 0`

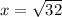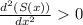
Thus, minima occurs at x =
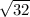`√(32)` for S(x).

If c be the smaller of the two numbers that minimize the sum, then,

`c = √(32) = 4\sqrt2\\\\S'(c) = 1 - \displaystyle(32)/(32) = 0\\\\S''(c) = (64)/(32√(32)) = (1)/(2\sqrt2)`