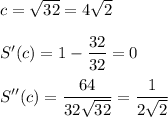Answer:
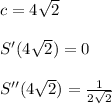
Explanation:
We are given the following information in the question:
The product of two numbers is 32.
Let the two numbers be x and y, then,
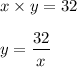
The sum of the two numbers = S(x)
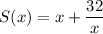
First, we differentiate S(x) with respect to x, to get,
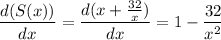
Equating the first derivative to zero, we get,
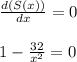
Solving, we get,
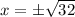
Again differentiation S(x), with respect to x, we get,
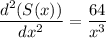
At
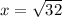 ,
,
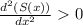
Thus, minima occurs at x =
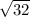 for S(x).
for S(x).
If c be the smaller of the two numbers that minimize the sum, then,