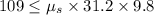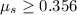Question

A girl exerts a horizontal force of 109 N on a crate with a mass of 31.2 kg. HINT (a) If the crate doesn't move, what's the magnitude of the static friction force (in N)? 109 Correct: Your answer is correct. The static friction force is fs ≤ μsn. For an object with no acceleration at rest on a surface, fs equals the particular value required to keep the object at rest on the surface. N (b) What is the minimum possible value of the coefficient of static friction between the crate and the floor? (Assume the crate remains stationary.)

Answer 1

(a) Magnitude of static friction force is 109 N

(b) Minimum possible value of static friction is 0.356

Solution:

As per the question;

Horizontal force exerted by the girl, F = 109 N

Mass of the crate, m = 31.2 kg

Now,

(a) To calculate the magnitude of static friction force:

Since, the crate is at rest, the forces on the crate are balanced and thus the horizontal force is equal to the frictional force, f:

F = f = 109 N

(b) The maximum possible force of friction between the floor and the crate is given by:

`f_(m) = \mu_(s)N`

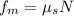
where

N = Normal reaction = mg

Thus

`f_(m) = \mu_(s)mg`

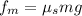
For the crate to remain at rest, The force exerted on the crate must be less than or equal to the maximum force of friction.

`f\leq f_(m)`

`f \leq \mu_(s)mg`

`109 \leq \mu_(s)* 31.2* 9.8`

`\mu_(s)\geq 0.356`