Question

You are taking a test in which items of type A are worth 10 points and items of type B are worth 15 points. It takes 3 minutes for each item of type A and 6 minutes for an item of type B. Total time allowed is 60 minutes, and you may answer more than 16 questions. Assuming all your answers are correct, how many items of each type should you answer in order to get the best score?

Answer 1

The best score is 200 points, answering 20 items of type A.

Explanation:

Let the following variables be:

x: items of type A

y: items of type B

The first condition is that it takes 3 minutes for each item of type A and 6 minutes for an item of type B. Total time allowed is 60 minutes. The equation would be:

`3x + 6y \leq 60\\ 6y \leq  60 -3x\\ y \leq  10 - (1)/(2)  x`

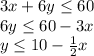
Furthermore, you may answer more than 16 questions. The second equation would be:

`x + y \geq 16\\ y \geq  16 -x`

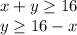
We show the plots of both equations in the attached pictures we find 3 critical points:

P₁ (16,0); P₂ (12,4); P₃ (20,0)

The score of the test would be:

S= 10x + 15y

We evaluate the points

P₁ (16,0)

S(16,0)= 10×16 + 15×0=160 points

P₂ (12,4)

S(16,0)= 10×12 + 15×4=180 points

P₃ (20,0)

S(20,0)= 10×20+ 15×0=200 points