Question

If given the equation x = -1/8(y + 6)^2 + 2 what is the location of the focus point PLEASE HELP

Answer 1

Focus is at
`(0,-6)`.

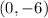Explanation:

Given:

The equation of the parabola is:
`x=-(1)/(8)(y+6)^(2)+2`

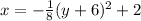
The standard form of a parabola in vertex form is given as:

`(y-k)^(2)=4p(x-h)`

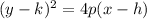
Where,
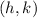`(h,k)` is the vertex of parabola. The value of
`p` decides the nature of parabola.

If
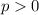`p >0`, the parabola opens rightwards and if
`p<0`, the parabola opens leftwards.

Let us first rewrite the given equation in standard form.

`x=-(1)/(8)(y+6)^(2)+2\\x-2=-(1)/(8)(y+6)^(2)\\-8(x-2)=(y+6)^(2)\\(y-(-6))^(2)=4(-2)(x-2)`

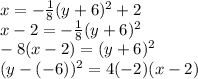
On comparing the above equation with the standard one, we get,

`h=2,k=-6,p=-2`

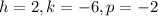
Therefore, the focus of a parabola of the form
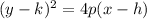`(y-k)^(2)=4p(x-h)` is given by the point
`(h+p,k)`.

∴ Focus is
`(h+p,k)=(2-2,-6)=(0,-6)`