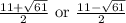The two values of roots of the polynomial
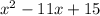 are
are
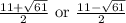
Solution:
Given, polynomial expression is
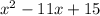
We have to find the roots of the given expression.
In order to find roots, now let us use quadratic formula.
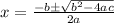
Given that
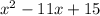
Here a = 1, b = -11 and c = 15
On substituting the values we get,
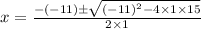
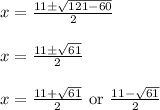
Hence, the roots of given polynomial are