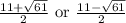Question

Which two values of x are roots of the polynomial below?
x2-11x + 15

Answer 1

The two values of roots of the polynomial
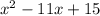`x^(2)-11 x+15` are
`(11+√(61))/(2) \text { or } (11-√(61))/(2)`

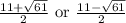
Solution:

Given, polynomial expression is
`x^(2)-11 x+15`

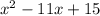
We have to find the roots of the given expression.

In order to find roots, now let us use quadratic formula.

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

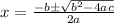
Given that
`x^(2)-11 x+15`

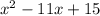
Here a = 1, b = -11 and c = 15

On substituting the values we get,

`x=\frac{-(-11) \pm \sqrt{(-11)^(2)-4 * 1 * 15}}{2 * 1}`

`\begin{array}{l}{x=(11 \pm √(121-60))/(2)} \\\\ {x=(11 \pm √(61))/(2)} \\\\ {x=(11+√(61))/(2) \text { or } (11-√(61))/(2)}\end{array}`

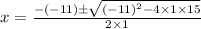
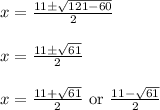
Hence, the roots of given polynomial are
`(11+√(61))/(2) \text { or } (11-√(61))/(2)`