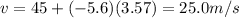1) 3.57 s
The motion of the frisbee is a uniformly accelerated motion, so we can use the suvat equation:

where
s is the displacement
u is the intiial velocity
t is the time
a is the acceleration
Here we have
s = 125 m (distance travelled)
u = 45 m/s (initial velocity)
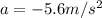 (deceleration of the frisbee)
(deceleration of the frisbee)
Substituting into the equation, we get
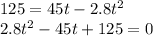
The solution of this equation are:
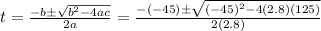
Which gives two solutions:
t = 3.57 s
t = 12.50 s
So, the frisbee crosses the point at distance d = 125 m from Phoebe two times: at 3.57 s the first time, then if it is free to move, the frisbee continues its motion and then at some point moves back to this point at t = 12.5 s. Since we are interested in the time at which Mike caught the frisbee, we just take the first solution:
t = 3.57 s
2) 25 m/s
Since this is a uniformly accelerated motion, the velocity of the frisbee is given by

where we have
u = 45 m/s is the initial velocity
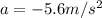 is the acceleration of the frisbee
is the acceleration of the frisbee
Since the frisbee has been caught at time
t = 3.57 s
We can substitute this value into the equation to find the final velocity of the frisbee: