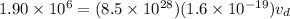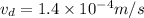1.
Answer:
Part a)
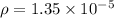
Part b)
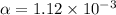
Step-by-step explanation:
Part a)
Length of the rod is 1.60 m
diameter = 0.550 cm
now if the current in the ammeter is given as
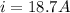
V = 17.0 volts
now we will have
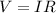
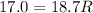
R = 0.91 ohm
now we know that
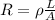
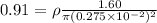
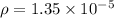
Part b)
Now at higher temperature we have
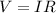
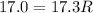
R = 0.98 ohm
now we know that
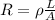
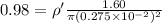
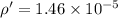
so we will have
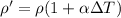
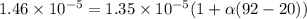
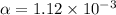
2.
Answer:
Part a)
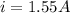
Part b)
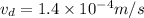
Step-by-step explanation:
Part a)
As we know that current density is defined as
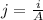
now we have
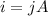
Now we have
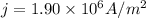
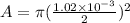
so we will have
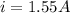
Part b)
now we have
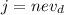
so we have
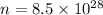

so we have