Question

a boy scout on top of a 1700 foot tall mountain spots a campsite. if he measures the angle of depression at 35°, how far is the campsite from the foot of the mountain

Answer 1

1190.35 ft

Explanation:

The figure for the given scenario is shown below.

From the triangle Δ ABC, AB is the height of mountain, BC is the distance of campsite from the foot of mountain and
`\angle A` is the depression angle.

So,
`AB=1700\textrm{ ft},\angle A=35`°

Let the side BC be
`x` ft.

Now, the tan of the angle A is given as:

`\tan (\angle A) =(BC)/(AB)`

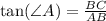
Plug in
`x` for BC, 1700 ft for AB and 35° for
`\angle A`. Solve for
`x`. This gives,

`\tan (35)=(x)/(1700)\\x=1700* \tan (35)=1190.35\textrm{ ft}`

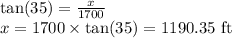
Therefore, the distance of campsite from the foot of the mountain is 1190.35 ft.