Answer:
A)
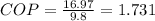
B)
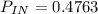
C) Second law efficiency 4.85%
exergy destruction for the cycle = 9.3237 kW
Step-by-step explanation:
Given data:
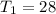 degree celcius
degree celcius
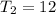 degree celcius
degree celcius
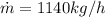
Power to refrigerator = 9.8 kW
Cp = 3.35 kJ/kg degree C
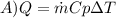
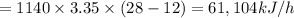

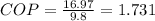
b)
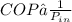
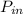 wil be max when COP maximum
wil be max when COP maximum
taking surrounding temperature T_H = 20 degree celcius
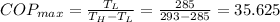
we know that
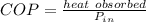
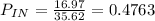
c) second law efficiency
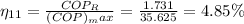
exergy destruction os given as
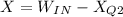
= 9.8 - 0.473 = 9.3237 kW