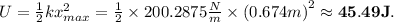Question

Tendons are strong elastic fibers that attach muscles to bones. To a reasonable approximation, they obey Hooke's law. In laboratory tests on a particular tendon, it was found that, when a 245g object was hung from it, the tendon stretched 1.20cm .(answer in N/m)

Find the force constant of this tendon in .
Because of its thickness, the maximum tension this tendon can support without rupturing is 135 N. By how much can the tendon stretch without rupturing, and how much energy is stored in it at that point? (answer in cm)

Answer 1

The elastic constant of this tendon is 200.2875 N/m. It can stretch up to 67.4 cm without rupturing, approximately; at this point, the tendon stores 45.49 J.

Step-by-step explanation:

From the Hooke's law in scalar form,
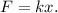`F=kx.`, we have

`k = (0.245 kg* 9.81(m)/(s^2))/(0.012 m) = \mathbf{200.2875 (N)/(m)}.`

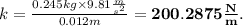
Now, the maximum strecht can be found from the same equation, by simply writing for
`x` and pluging in the maximun tension, i.e.,

`x_(max) = (F_(max))/(k) = (135 N)/(200.2875 (N)/(m)) \approx 0.674 m \approx \mathbf{67.4 cm} .`

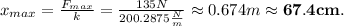
The energy stored in this tendon, at this point, comes from

`U = (1)/(2)kx_(max)^2 = (1)/(2)* 200.2875 (N)/(m) * \left(0.674 m\right)^2 \approx \mathbf{45.49 J}.`