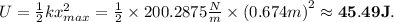Answer:
The elastic constant of this tendon is 200.2875 N/m. It can stretch up to 67.4 cm without rupturing, approximately; at this point, the tendon stores 45.49 J.
Step-by-step explanation:
From the Hooke's law in scalar form,
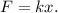 , we have
, we have
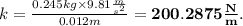
Now, the maximum strecht can be found from the same equation, by simply writing for
 and pluging in the maximun tension, i.e.,
and pluging in the maximun tension, i.e.,
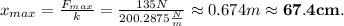
The energy stored in this tendon, at this point, comes from