Question

You are to drive to an interview in another town, at a distance of 270 km on an expressway. The interview is at 11:15 a.m. You plan to drive at 100 km/h, so you leave at 8:00 a.m. to allow some extra time. You drive at that speed for the first 110 km, but then construction work forces you to slow to 42.0 km/h for 43.0 km. What would be the least speed needed for the rest of the trip to arrive in time for the interview?

Answer 1

To reach on time, after the delay, the student must drive the remaining 117 km at a least speed of 104 km/h.

Step-by-step explanation:

The student needs to calculate the least speed needed to complete the remaining distance on time after encountering a delay due to construction work. To solve this, we will divide the problem into three parts, calculating the time spent on each segment and determining the remaining time available for the final segment.

Calculations:

• Time for the first 110 km at 100 km/h: 110 km / 100 km/h = 1.1 hours.
• Time for the 43.0 km at 42.0 km/h: 43 km / 42 km/h = 1.024 hours.
• Total time used so far: 1.1 + 1.024 = 2.124 hours.
• Total time available: 11:15 a.m. - 8:00 a.m. = 3.25 hours.
• Time remaining for the last segment: 3.25 - 2.124 = 1.126 hours.
• Distance remaining: 270 km - (110 km + 43 km) = 117 km.
• Least speed needed: 117 km / 1.126 hours = 103.9 km/h, rounded up to 104 km/h to ensure on-time arrival.

Therefore, to arrive in time for the interview, the student must drive at a least speed of 104 km/h for the rest of the trip.

Answer 2

the least required speed is 103.88 km/h

Step-by-step explanation:

Data provided in the question:

Total distance = 270 km

Total time to reach = Time between 8 a.m and 11:15 a.m i.e 3.25 hours

Now,

For the distance of 110 km speed was 100 km/h

therefore, the time taken to cover 110 km =
`\frac{\textup{Distance}}{\textup{speed}}`

=
`\frac{\textup{110 km}}{\textup{100 km/h}}`

= 1.1 hour

For another 43 km speed was 42 km/h

therefore, the time taken to cover 43 km =
`\frac{\textup{Distance}}{\textup{speed}}`

=
`\frac{\textup{43 km}}{\textup{42 km/h}}`

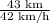
= 1.0238 hours

Now,

The distance left to be covered = 270 - 110 - 43 = 117 km

Time left = 3.25 h - 1.1 h - 1.0238 h = 1.1262 h

Thus required speed =
`\frac{\textup{117 km}}{\textup{1.1262 h}}`

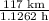
= 103.88 km/h

Hence, the least required speed is 103.88 km/h