Question

Two possible solutions of √11-2x=√x^2+4x+4 are –7 and 1. Which statement is true? A) Only x = –7 is an extraneous solution.

B) Only x = 1 is an extraneous solution.
C) Both solutions are extraneous.
D)Neither solution is extraneous.

Answer 1

Answer:D

Explanation:

Answer 2

Option D)Neither solution is extraneous.

Explanation:

we have

`√(11-2x)=\sqrt{x^(2)+4x+4}`

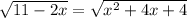
we know that

two possible solutions are x=-7 and x=1

Verify each solution

Substitute each value of x in the expression above and interpret the results

1) For x=-7

`√(11-2(-7))=\sqrt{-7^(2)+4(-7)+4}`

`√(25)=√(25)`

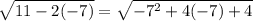
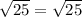
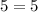`5=5` ----> is true

therefore

x=-7 is not a an extraneous solution

2) For x=1

`√(11-2(1))=\sqrt{1^(2)+4(1)+4}`

`√(9)=√(9)`

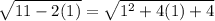
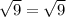
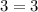`3=3` ----> is true

therefore

x=1 is not a an extraneous solution

therefore

Neither solution is extraneous