Answer:
Option D)Neither solution is extraneous.
Explanation:
we have
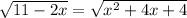
we know that
two possible solutions are x=-7 and x=1
Verify each solution
Substitute each value of x in the expression above and interpret the results
1) For x=-7
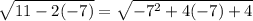
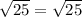
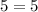 ----> is true
----> is true
therefore
x=-7 is not a an extraneous solution
2) For x=1
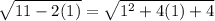
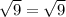
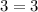 ----> is true
----> is true
therefore
x=1 is not a an extraneous solution
therefore
Neither solution is extraneous