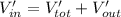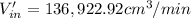Question

Water is leaking out of an inverted conical tank at a rate of 11700.0 cubic centimeters per min at the same time that water is being pumped into the tank at a constant rate. The tank has height 14.0 meters and the diameter at the top is 5.0 meters. If the water level is rising at a rate of 20.0 centimeters per minute when the height of the water is 2.5 meters, find the rate at which water is being pumped into the tank in cubic centimeters per minute.

Answer 1

`V'_(in)=136,922.92cm^(3)/min`

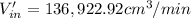
Step-by-step explanation:

In order to solve this problem, we must start by drawing the situation so we can see what the problem is about. (See attached picture)

So, since the problem wants us to write our answer in centimeters per minute, we can start by converting each of the meters to centimeters,so we get:

`5m*(100cm)/(1m)=500cm`

`14m*(100cm)/(1m)=1400cm`

`2.5m*(100cm)/(1m)=250cm`

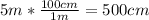
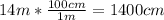
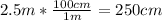
Next, the volume of a cone can be found by using the following formula:

`V=(1)/(3) \pi r^(2)h`

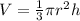
In this case, both the radius and the height will be constantly changing, so we will need to find an equation to relate the height with the radius. We can find it by analyzing the cross section of the cone, which makes a right triangle. By using similar triangles we get:

`(h)/(r)=(1400)/(250)`

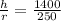
when solving for r we get that:

`r=(250)/(1400) h`

which simplifies to:

`r=(5)/(28) h`

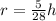
so now, we can substitute this on our volume equation so we get:

`V=(1)/(3) \pi ((5)/(28)h)^(2)h`

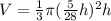
which simplifies to:

`V=(25)/(2352)\pi h^(3)`

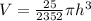
now we can take the derivative of that equation so we get:

`(dV)/(dt)=(25)/(784)\pi h^(2) (dh)/(dt)`

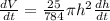
and now we can substitute:

`(dV)/(dt)=(25)/(784)\pi (250cm)^(2) (20cm/min)`

which solves to

`(dV)/(dt)=125,222.92(cm^(3))/(min)`

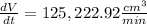
this will represent the total amount of water that is being kept inside the tank. Now we can calculate the amount of water that is entering the tank.

`V'_(in)-V'_(out)=V'_(tot)`

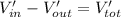
so:

`V'_(in)=V'_(tot)+V'_(out)`

`V'_(in)=125,222.92cm^(3)/min+11,700cm^(3)/min`

`V'_(in)=136,922.92cm^(3)/min`