Answer:
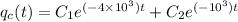
Explanation:
given,
C = 0.25 × 10⁻⁶ F
R = 5 × 10³ F
L = 1 H
E = 24
the equation of the circuit
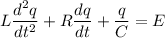
substitute the given data
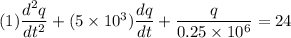
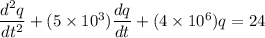
auxiliary equation
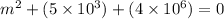
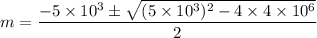
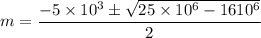
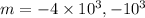
so, complimentary function
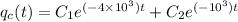
charge at any time t is given by the above equation.
C₁ and C₂ are arbitrary constant
which will be calculated using boundary condition.