Question

What are the solution(s) to the quadratic equation 9x2 = 4? x = StartFraction 4 Over 9 EndFraction and x = StartFraction negative 4 Over 9 EndFraction x = StartFraction 2 Over 3 EndFraction and x = StartFraction negative 2 Over 3 EndFraction x = StartFraction 3 Over 2 EndFraction and x = StartFraction negative 3 Over 2 EndFraction no real solution

Answer 1

`S=\left \{x \in\mathbb{R}| x= \pm (2)/(3) \right \}`

Or

x = StartFraction negative 2 Over 3 EndFraction.

Explanation:

As in this quadratic equation, b and c parameters are equal to zero. We can simply divide everything by 9 and then take the square root of all members of this equation. This equation has two solutions since Δ > 0, so we can write the solution formally as
`S=\left \{x \in\mathbb{R}| x= \pm (2)/(3) \right \}`

`9x^(2)=4\\(9x^(2))/(9)=(4)/(9)\Rightarrow x^(2)=(4)/(9)\Rightarrow \sqrt{x^(2)}=\sqrt{(4)/(9)}\\x=\pm (2)/(3)\Rightarrow S=\left \{x \in\mathbb{R}| x= \pm (2)/(3) \right \}`

Answer 2

x = StartFraction 2 Over 3 EndFraction and x = StartFraction negative 2 Over 3 EndFraction.

Step-by-step explanation:

We are given a quadratic equation of single variable x as
`9x^(2) =4`.

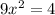There is no doubt that as the equation is of two degrees so, it will have two solutions.

Now,
`9x^(2) =4`

⇒
`x^(2) =(4)/(9)`

⇒
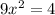
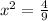
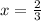`x=(2)/(3)` and
`x = -(2)/(3)`

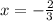
Therefore, the solution will be x = StartFraction 2 Over 3 EndFraction and x = StartFraction negative 2 Over 3 EndFraction. (Answer)