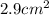Answer:
Explanation:
Given,
Angle of sector = 30°
Radius of circle, r = 8 cm
Area of the shaded region, A =?
The diagram is attached below.
Now,
Area of shaded region = Area of sector - Area of triangle
Area of triangle =
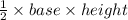
We know that,
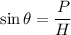
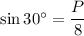
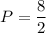
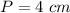
And

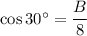
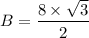
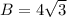
Area of sector =
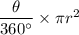
Area of sector =
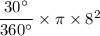
= 16.75 cm^2
Area of triangle =
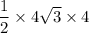
= 13.85 cm^2
Area of shaded region = 16.75 - 13.85
=