Question

Use the NRCS lag equation to estimate the lag time for a watershed characterized by a curve number of 75 and an average watershed slope of 2.8 percent. The distance along the flow path from the outlet to the furthest point on the watershed divide measured from a topographic map is 2,100 m (6,900 ft). Estimate the time of concentration for the watershed. (Answer: tc -= 1.72 hours)

Answer 1

Tc = 1.722 h

Step-by-step explanation:

given data

curve number CN = 75

slope y= 2.8 %

distance l = 2,100 m (6,900 ft)

to find out

time of concentration for the watershed

solution

we calculate here time of concentration by NRCS lag method is

Tc =
`(L)/(0.6)`

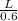
and here

L =
`\frac{l^{0.8(S + 1)^(0.7)}}{1900y^(0.5)}`

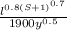
here

L is lag time

l is flow length

and y is average water slop

and S is maximum potential retention

so here S =
`(1000)/(CN) - 10`

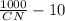
so here CN is NRCS curve no

so put here value

S =
`(1000)/(75) - 10` = 3.33

and

L =
`\frac{l^{0.8(S + 1)^(0.7)}}{1900y^(0.5)}`

L =
`\frac{6900^{0.8(3.33 + 1)^(0.7)}}{1900*2.8^(0.5)}`

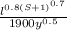
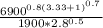
L = 1.033 h

so

Tc =
`(1.033)/(0.6)`

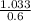
Tc = 1.722 h