Answer:
The pair of equations is consistent
Explanation:
A consistent system of equations has at least one solution
- The consistent independent system has exactly 1 solution
- The consistent dependent system has infinitely many solutions
An inconsistent system has no solution
In the system of equations ax + by = c and dx + ey = f, if
- a = d, b = e, and c = f, then the system is consistent dependent and has infinitely many solutions
- a = d, b = e, and c ≠ f, then the system is inconsistent and has no solution
- a ≠ d, and/or b ≠ e, and/or c ≠ f, and
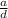 ≠
≠
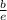 , then the system is consistent independent and has exactly one solution
, then the system is consistent independent and has exactly one solution
∵ x - 2y = 0
∴ The coefficient of x ⇒ a = 1
∴ The coefficient of y ⇒ b = -2
∴ The numerical term ⇒ c = 0
∵ 3x + 4y - 20 = 0
→ Add 20 to both sides
∴ 3x + 4y - 20 + 20 = 0 + 20
∴ 3x + 4y = 20
∵ The coefficient of x ⇒ d = 3
∵ The coefficient of y ⇒ e = 4
∵ The numerical term ⇒ f = 20
∵ a ≠ d
∵ b ≠ e
∵ c ≠ f
∵
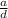 =
=

∵
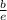 =
=
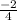 =
=
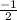
∴
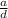 ≠
≠
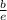
→ By using rule 3 above
∴ The pair of equations is consistent