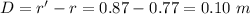Answer:
The path separation is 0.10 m
Solution:
As per the question:
Mass of
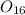 , m =
, m =
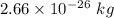
Ratio of the masses, R = 16:18
Velocity, v =
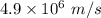
Magnetic field, B = 1.05 T
Now,
Mass of
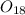 , m' = m\frac{1}{R} = 2.66\times 10^{- 26}\times \frac{18}{16} = 2.99\times 10^{- 26}\ kg[/tex]
, m' = m\frac{1}{R} = 2.66\times 10^{- 26}\times \frac{18}{16} = 2.99\times 10^{- 26}\ kg[/tex]
Now, centripetal force here is provided by the magnetic force on the charge 'q' and is given by:
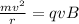
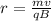
Now, for
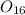 :
:
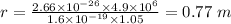
Now, for
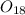 :
:
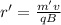
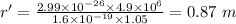
Now, the separation distance of the path is given by: