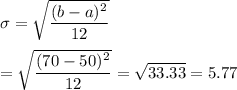Question

The cycle time for trucks hauling concrete to a highway construction site is uniformly distributed over the interval 50 to 70 minutes.

a. What is the probability that a given cycle time will be less than 65 minutes?
b. What is the probability that the cycle time is less than 65 minutes if it is known that the cycle time exceeds 55 minutes?
c. Find the mean and variance of the cycle time for the trucks.

Answer 1

a) 0.75

b) 0.5

c) Mean = 60 minutes

Standard Deviation = 5.77 minutes

Explanation:

We are given the following information in the question:

The cycle time for trucks hauling concrete to a highway construction site is uniformly distributed over the interval 50 to 70 minutes.

a = 50, b = 70

`f(x) = \displaystyle(1)/(b-a) = (1)/(70-50) = (1)/(20)`

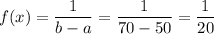
We are given a uniform distribution.

a) P(cycle time will be less than 65 minutes)

P( x < 65)

`=\displaystyle\int_(65)^(50) f(x) dx\\\\=\displaystyle\int_(65)^(50) (1)/(20)dx\\\\=(1)/(20)[x]_(65)^(50) = (1)/(20)(65-50) = 0.75`

b) P(cycle time is less than 65 minutes if it is known that the cycle time exceeds 55 minutes)

P( 55 < x < 65)

`=\displaystyle\int_(65)^(55) f(x) dx\\\\=\displaystyle\int_(65)^(55) (1)/(20)dx\\\\=(1)/(20)[x]_(65)^(55) = (1)/(20)(65-55) = 0.5`

c) Mean:

`\mu = \displaystyle(a+b)/(2)\\\\\mu = (50+70)/(2) = 60`

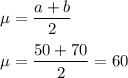
Standard Deviation:

`\sigma = \sqrt{\displaystyle((b-a)^2)/(12)}\\\\= \sqrt{\displaystyle((70-50)^2)/(12)} = √(33.33) = 5.77`