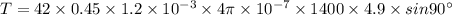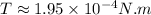Answer:
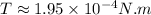
Step-by-step explanation:
Given:
A long solenoid having
no. of turns per meter, n =1400
current, I = 4.9 A
A small coil of wire placed inside the solenoid
angle of orientation with respect to the axis of the solenoid,
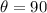 °
°
no. of turns in the coil, N = 42
area of the coil,

current in the coil,

We have for torque:
 .......................(1)
.......................(1)
∵
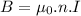 ................................(2)
................................(2)
where:
B= magnetic field
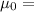 The permeability of free space =
The permeability of free space =
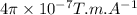
Substitute B from eq. (2) into eq. (1) we have:
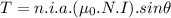
putting the respective values in above eq.