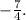For this case we have the following functions:
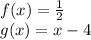
We must find
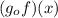 . For definition of composition of functions we have to:
. For definition of composition of functions we have to:
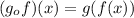
So:
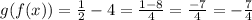
Then, for any value of "x", the composite function has a value of
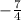 .
.
Thus,
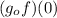 cannot be evaluated, it will always be obtained
cannot be evaluated, it will always be obtained
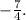
ANswer:
For any value of "x", the composite function has a value of